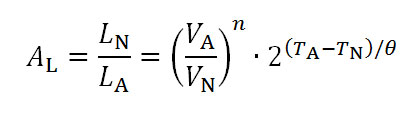一般来说贴片电容的加速度实验是通过对电压和温度的加速来进行的。并以实验中测定的温度电压等数据作为参数运用下面的加速公式推算出产品在实际使用环境下的使用寿命。
下面的加速公式是基于阿列纽斯法，利用电压加速系数（※1）及反应活化能（※2）推算。



在此公式的基础上，通过在更为严苛的条件(更高温、更高电压)下进行加速试验，可推算出产品在实际使用环境下的使用寿命。

为了简化计算我们也会通过如下的加速计算公式进行计算。


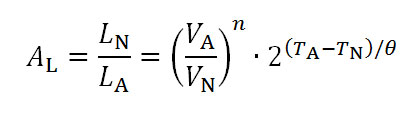
在试验温度为TA时的故障率是标准温度TN时的故障率的1/2（或者是2 倍），我们将其温度差θ（=TA-TN）称作温度加速系数。 我们把加载电压固定，将温度设为参数来进行MlCC的试验样本的寿命试验，把各个温度条件下的试验结果（故障率）通过计算公式计算出温度加速系数。


在此我们一起来比较一下贴片电容的加速试验与实际产品使用的假定环境。我们将贴片电容器的加速试验中将耐久试验时间视为LA，将实际使用环境下的相当年数视为LN，用于上述公式。

耐久试验条件	假定使用环境	电压加速系数	温度加速系数	相应年限
TA＝85°C VA＝20V LA＝1000h	TN＝65°C VN＝5V	n＝3	θ＝8	LN＝?h

这样我们即可通过在85°C、施加20V电压的环境下进行了1000h的耐久试验，推算出在65°C、施加5V电压的环境下产品使用年限为362039h（≒41年！）。计算中使用的电压加速系数、温度加速系数会由陶瓷材料的种类及构造产生不同，但通过加速计算公式可在相对较短的时间内利用试验结果来验证长时间的实际使用环境中的产品使用寿命。

※1 电压加速系数的推算方法的相关说明

在推算贴片电容的产品寿命时，我们把实验温度固定，将加载电压设为参数来进行MlCC的试验样本的寿命试验。把各个加载电压下的试验结果（平均寿命MTTF）通过韦伯分析方法近似推算加载电压对数与平均寿命对数的斜率/并将其作为电压加速系数。

※2 反应活化能的推算方法的相关说明

和上述温度加速系数的推算方法类似，我们把加载电压固定，将实验温度设为参数来进行MlCC的试验样本的寿命试验。把各个实验温度下的试验结果（平均寿命MTTF）通过韦伯分析方法近似推算温度（绝对温度）的倒数与平均寿命对数的斜率，并将其作为反应活化能。